Vectorization in Python: Replace Loops with 100-1000x Faster Array Operations

Adril Lee . 6min read

Feb. 05 2025

Vectorization in Python: The End of Loops for Large-Scale Data Processing

Discover how replacing traditional loops with vectorized operations can accelerate your Python code by 100-1000x when working with massive datasets.

Data visualization showing massive parallel processing versus linear processing — The paradigm shift: from sequential processing (left) to parallel vectorized operations (right)

The Vectorization Revolution: Parallel vs Sequential Processing

Vectorization represents one of the most significant performance optimizations in modern data science. At its core, it's about replacing sequential element-by-element operations with parallel array processing, leveraging optimized low-level libraries (primarily written in C and Fortran) that process entire datasets simultaneously.

Traditional Loop Processing

Process element 1

Process element 2

Process element 3

...

Process element N

Execution: Sequential, one element at a time
Overhead: Python interpreter overhead per iteration
Memory: Frequent cache misses
Speed: O(N) with high constant factors

Vectorized Processing

Element 1

Element 2

Element 3

...

Element N

Execution: Parallel, all elements simultaneously
Overhead: Single optimized C/Fortran function call
Memory: Cache-friendly contiguous operations
Speed: O(N) with minimal constant factors

Why Vectorization is Faster:

SIMD Instructions: Modern CPUs support Single Instruction, Multiple Data operations
Reduced Python Overhead: One function call instead of N interpreter operations
Memory Locality: Contiguous array operations are cache-optimized
Parallel Hardware: Leverages multiple CPU cores and vector registers

Benchmark 1: Summing 1.5 Million Numbers

Let's start with a fundamental operation: summing a sequence of numbers. This demonstrates the most basic vectorization principle.

Traditional Loop Approach

Python Time: 0.14 seconds

import time

start = time.time()
total = 0

# Iterating through 1.5 million numbers
for item in range(0, 1500000):
    total = total + item

print(f'Sum: {total}')
end = time.time()
print(f'Time: {end - start:.3f} seconds')
# Output: 1124999250000
# Time: 0.140 seconds

Performance Issues:

1.5 million Python interpreter iterations
Type checking and boxing/unboxing each iteration
Function call overhead for each addition
Poor cache utilization

Vectorized NumPy Approach

NumPy Time: 0.008 seconds

import numpy as np
import time

start = time.time()

# Vectorized sum in single operation
result = np.sum(np.arange(1500000))

print(f'Sum: {result}')
end = time.time()
print(f'Time: {end - start:.3f} seconds')
# Output: 1124999250000
# Time: 0.008 seconds

Performance Advantages:

Single C-level function call
Contiguous memory operations
SIMD CPU instructions
Minimal Python interpreter overhead

Performance Improvement: 18x Faster

This basic example shows vectorization delivering an 18x speed improvement. The gap widens dramatically with more complex operations and larger datasets.

Benchmark 2: DataFrame Mathematical Operations

Creating the Test Dataset

Pandas/NumPy 5 Million Rows × 4 Columns

import numpy as np
import pandas as pd

# Create DataFrame with 5 million rows, 4 columns
# Values are random integers between 0 and 50
df = pd.DataFrame(
    np.random.randint(0, 50, size=(5000000, 4)),
    columns=('a', 'b', 'c', 'd')
)

print(f'DataFrame shape: {df.shape}')
print(df.head())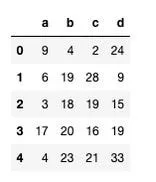

First 5 rows of 5 million row DataFrame — The test DataFrame: 5 million rows of random integer data

Task: Create Ratio Column (d ÷ c × 100)

Loop Approach: DataFrame.iterrows()

Python Loop Time: 109 seconds

import time

start = time.time()

# Iterating through DataFrame using iterrows
for idx, row in df.iterrows():
    # Calculate ratio for each row individually
    df.at[idx, 'ratio'] = 100 * (row["d"] / row["c"])

end = time.time()
print(f'Time: {end - start:.2f} seconds')
# Time: 109.00 seconds

Critical Performance Issues:

iterrows() creates Series objects for each row
df.at[] has significant overhead per cell
5 million Python object creations
Row-by-row division and multiplication

Vectorized Approach: Column Operations

Vectorized Pandas Time: 0.12 seconds

import time

start = time.time()

# Vectorized operation on entire columns
df["ratio"] = 100 * (df["d"] / df["c"])

end = time.time()
print(f'Time: {end - start:.3f} seconds')
# Time: 0.120 seconds

Vectorization Benefits:

Single operation on entire columns
NumPy array operations underneath
Memory-efficient contiguous processing
Automatic handling of NaN/inf values

Performance Improvement: 908x Faster

This demonstrates why vectorization is non-negotiable for DataFrame operations. The 900x speed difference transforms what would be minutes of waiting into instant results.

Benchmark 3: Conditional Logic with Vectorization

The Conditional Column Challenge

Create column 'e' based on conditions in column 'a':

If a == 0: e = d
If 0 < a ≤ 25: e = b - c
Otherwise: e = b + c

Loop with Conditional Logic

Python Loop + Conditions Time: 177 seconds

import time

start = time.time()

for idx, row in df.iterrows():
    if row.a == 0:
        df.at[idx, 'e'] = row.d    
    elif (row.a <= 25) & (row.a > 0):
        df.at[idx, 'e'] = row.b - row.c    
    else:
        df.at[idx, 'e'] = row.b + row.c

end = time.time()
print(f'Time: {end - start:.2f} seconds')
# Time: 177.00 seconds

Vectorized Conditional Logic

Pandas Vectorized Conditions Time: 0.28 seconds

import time

start = time.time()

# Start with default case
df['e'] = df['b'] + df['c']

# Apply conditions using vectorized indexing
df.loc[df['a'] <= 25, 'e'] = df['b'] - df['c']
df.loc[df['a'] == 0, 'e'] = df['d']

end = time.time()
print(f'Time: {end - start:.3f} seconds')
# Time: 0.280 seconds

The Vectorized Conditional Pattern:

# Pattern: Start with default, then apply conditions
df['result'] = default_value                    # Default case
df.loc[condition1, 'result'] = value1          # Condition 1
df.loc[condition2, 'result'] = value2          # Condition 2
# ... additional conditions as needed

Benefits of This Pattern:

Avoids nested if-else logic: Clear, sequential conditions
Maintains vectorization: Each condition processes entire subsets
Readable and maintainable: Conditions are explicit and separate
Optimized execution: Pandas optimizes sequential .loc operations

Performance Improvement: 632x Faster

Conditional logic shows even greater benefits from vectorization, transforming nearly 3 minutes of processing into under 300 milliseconds.

Benchmark 4: Machine Learning Operations

The Linear Regression Computation

For a simple linear regression prediction: y = m₁x₁ + m₂x₂ + m₃x₃ + m₄x₄ + m₅x₅

We need to compute this for 5 million data points with 5 features each.

Nested Loop Computation

Double Nested Loops Time: 28.23 seconds

import numpy as np
import time

# Model parameters and input data
m = np.random.rand(1, 5)            # 1×5 parameter vector
x = np.random.rand(5000000, 5)      # 5M×5 feature matrix
y = np.zeros(5000000)               # Output vector

tic = time.process_time()

# Nested loops for dot product
for i in range(5000000):
    total = 0
    for j in range(5):
        total += x[i][j] * m[0][j]
    y[i] = total

toc = time.process_time()
print(f"Time: {toc - tic:.3f} seconds")
# Time: 28.228 seconds

Vectorized Matrix Multiplication

NumPy Dot Product Time: 0.107 seconds

import numpy as np
import time

# Same data setup
m = np.random.rand(1, 5)
x = np.random.rand(5000000, 5)

tic = time.process_time()

# Single vectorized operation
y = np.dot(x, m.T)  # or x @ m.T in Python 3.5+

toc = time.process_time()
print(f"Time: {toc - tic:.3f} seconds")
# Time: 0.107 seconds

Why NumPy.dot is So Fast:

1. BLAS/LAPACK Integration

NumPy delegates to optimized linear algebra libraries (OpenBLAS, MKL, ATLAS) that use:

CPU-specific SIMD instructions (AVX, SSE)
Multi-threaded parallel processing
Cache-optimized memory access patterns

2. Memory Hierarchy Optimization

# Memory access patterns:
Loop approach:     x[0][0], x[0][1], x[0][2]...  # Poor locality
Vectorized:        x[0:block][0:block]           # Contiguous blocks

3. Reduced Python Overhead

One C function call vs. 25 million Python operations (5M rows × 5 features)

Performance Improvement: 264x Faster

For machine learning operations, vectorization isn't just an optimization it's a requirement. The difference between 28 seconds and 0.1 seconds enables interactive model development.

The Vectorization Toolkit: Essential Patterns

1. Universal Functions (ufuncs)

# Instead of:
result = []
for x in array:
    result.append(math.sin(x))

# Use NumPy ufunc:
result = np.sin(array)  # 50-100x faster

Available ufuncs: np.sin, np.exp, np.log, np.sqrt, all arithmetic operators

2. Aggregation Operations

# Instead of:
total = 0
for x in data:
    total += x

# Use vectorized aggregation:
total = np.sum(data)      # sum
mean = np.mean(data)      # mean
std = np.std(data)        # standard deviation

Key insight: These operations have O(N) complexity but 100x smaller constant factors.

3. Boolean Masking

# Instead of:
filtered = []
for x in data:
    if condition(x):
        filtered.append(x)

# Use boolean indexing:
mask = data > threshold
filtered = data[mask]

Advanced: Combine masks with & (and), | (or), ~ (not)

4. Broadcasting

# Instead of:
for i in range(n):
    result[i] = array[i] + scalar

# Use broadcasting:
result = array + scalar  # Works for arrays of any dimension

Rule: Dimensions are aligned from the right, and missing dimensions are treated as size 1.

When NOT to Use Vectorization

1. Small Datasets

For datasets smaller than ~1,000 elements, the overhead of importing NumPy/Pandas and converting to arrays may outweigh benefits.

Guideline:

Use vectorization when N > 1000 or when operations are complex enough to justify setup time.

2. Complex Conditional Logic

When conditions involve complex function calls or external dependencies that can't be vectorized.

Alternative:

Use numba or numpy.vectorize() (with caution) for complex element-wise operations.

3. Memory Constraints

Vectorized operations often create intermediate arrays. If memory is tight, loops may be more memory-efficient.

Solution:

Use generator expressions or chunk processing for out-of-memory datasets.

Migrating from Loops to Vectorization

Step 1: Identify Loop Patterns

Common patterns that can be vectorized:

Element-wise operations: for x in data: result.append(f(x))
Aggregations: for x in data: total += x
Conditional transformations: Nested if-else in loops
Matrix operations: Nested loops for dot products

Step 2: Convert to NumPy/Pandas

Ensure data is in vectorizable format:

# Convert to NumPy array
list_data = [1, 2, 3, 4, 5]
array_data = np.array(list_data)  # Now vectorizable

# Ensure DataFrame columns are appropriate dtypes
df['column'] = df['column'].astype(np.float32)  # Faster than float64

Step 3: Apply Vectorized Operations

Replace loop logic with vectorized equivalents:

Before (Loop):

result = []
for x in data:
    if x > 0:
        result.append(x * 2)
    else:
        result.append(x / 2)

After (Vectorized):

result = np.where(data > 0, data * 2, data / 2)

Step 4: Profile and Optimize

Use profiling to identify remaining bottlenecks:

import timeit

# Time vectorized version
vectorized_time = timeit.timeit(
    "np.sum(data)", 
    setup="import numpy as np; data=np.random.rand(1000000)",
    number=100
)

# Compare with loop version (if necessary)
loop_time = timeit.timeit(
    "sum(x for x in data)", 
    setup="import numpy as np; data=list(np.random.rand(1000000))",
    number=100
)

print(f"Vectorized: {vectorized_time:.3f}s, Loop: {loop_time:.3f}s")

The Vectorization Mindset Shift

Think in Arrays, Not Elements

Instead of asking "what happens to this element?", ask "what operation applies to the entire array?"

Embrace Batch Processing

Design algorithms that process entire datasets in single operations, not row-by-row.

Learn the Vectorized Vocabulary

Master key NumPy/Pandas functions: np.where(), df.loc[], np.dot(), broadcasting, ufuncs.

Summary of Performance Gains:

Operation	Loop Time	Vectorized Time	Speedup
Sum 1.5M Numbers	0.140s	0.008s	18×
DataFrame Ratio	109.0s	0.120s	908×
Conditional Logic	177.0s	0.280s	632×
ML Dot Product	28.23s	0.107s	264×

Vectorization isn't just a performance optimization it's a different way of thinking about data processing. The most significant benefit isn't just the speed improvement (which is substantial), but the mental model shift from sequential to parallel thinking. This mindset serves you well not just in Python, but in understanding modern computing architecture, parallel processing, and efficient algorithm design.

Python Anaconda Vectorization Data Science